Community Articles
- Cloudera Community
- Support
- Community Articles
- Understanding the Logistic Regression Model in Pyt...
- Subscribe to RSS Feed
- Mark as New
- Mark as Read
- Bookmark
- Subscribe
- Printer Friendly Page
- Report Inappropriate Content
- Subscribe to RSS Feed
- Mark as New
- Mark as Read
- Bookmark
- Subscribe
- Printer Friendly Page
- Report Inappropriate Content
Created on 11-04-2019 07:52 AM - edited 11-05-2019 08:38 AM
Introduction
In this article we’re going to look at Logistic regression which is a technique widely used in industry to solve binary classification problems. Unlike the linear regression model, which is used to make predictions on the numerical target variable, logistic regression has the ability to deal with discrete valued outcomes. For example, a numerical target variable might involve predicting house prices, whereas a discrete valued outcome might involve predicting who would win in the next presidential elections. Logistic regression is most commonly used in solving binary classification problems, such as tumor detection, credit card fraud detection, email spam detection, and so on.
How the logistic regression model works
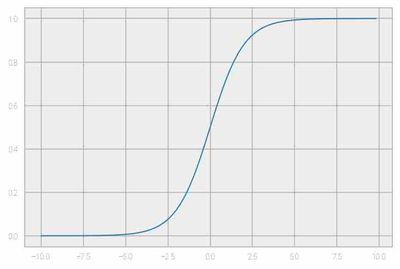
The logistic regression model makes use of the sigmoid function (also known as the logistic function) to measure the relationship between input variables and the output variable by estimating probability scores of the outcome. Unlike linear regression, logistic regression uses a different cost function by making use of a sigmoid function to make a prediction fall between 0 and 1.
What is a sigmoid function?
The main reason behind using a sigmoid function as the cost function is that it helps to map predicted values to probabilities that hold the values in the range 0 to 1. Equation used to represent a sigmoid function: 1/1+exp(-x). Plot of sigmoid function is shown as below.
Hypothesis representation of the logistic regression model
The hypothesis function in linear regression is represented as h(x)=β₀ + β₁X. In logistic regression, there is a slight modification to the hypothesis function, so that it becomes:
hθ(x) = 1/(1 + e^-(β₀ + β₁X)
The major change you can observe here is the use of an additional sigmoid function.
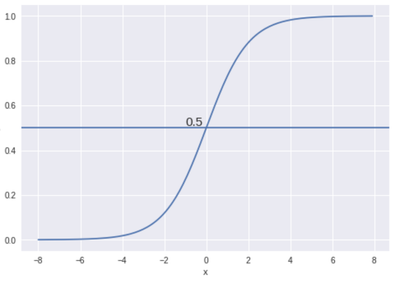
Decision boundary: We expect a logistic regression classifier to produce a set of outputs based on probability when we pass the inputs through a prediction function and it returns a probability score between 0 and 1. For example, if you have two classes—say, tumor and non-tumor samples—the logistic regression model decides on a threshold value, above which we classify values as class 1, and below which we classify as class 2.
Fig 1: Threshold
For example, in the figure above, 0.5 is considered the threshold. If the prediction function returned 0.7, then it is considered as class 1 (tumor). If the prediction function returned 0.2, then it is considered as class 2 (non-tumor).
Cost function: The cost function is responsible for calculating the error between the actual value and the predicted value. After the cost function is created, our goal is to minimize the error with an optimization function. In this article, we will discuss gradient descent optimization, which is widely used for this purpose.
For logistic regression, the cost function is defined as:
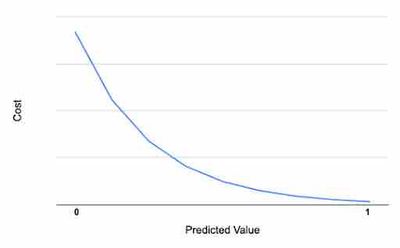
When the true value is 1 and the predicted value(y) is 1, the cost is zero. When the prediction is far away from 1, the cost increases as shown in the above image. In linear algebra, this type of function is represented as:
−log(hθ(x)) if y = 1
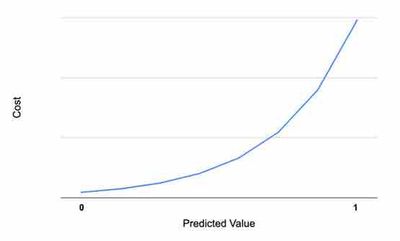
Similarly, when the actual value is 0 and the predicted value is exactly 0, the cost is 0. If the predicted value is moving far from the actual value, the cost increases as shown in the figure below. This type of plot in linear algebra is:
−log(1−hθ(x)) if y = 0
Gradient descent optimization
To minimize the cost function value, we will be looking into an optimization algorithm known as gradient descent. To minimize a cost function, we need to run the gradient descent function on each parameter. Below is the pseudo code used by gradient descent:
- Initialize the parameters
Repeat {
- Make a prediction on y
- Calculate cost function
- Get gradient for cost function
- Update parameters
}
Sample implementation of logistic regression
Let’s look into the pseudo code for important steps in building a logistic regression model with Python’s powerful scikit-learn library.
Load a dataset: Import all the necessary steps and load the dataset into a dataframe.
Apply feature scaling: Feature scaling is important to standardize data that feeds a model.
Train_test split function: Splits the data into a training set and a test set.
Fit the logistic regression model: Instantiate the logistic regression model and train the model with the data.
Prediction and testing: Predict the test set data using the trained model.
Evaluation of metrics: Evaluate metrics with a confusion matrix, precision/recall, or f-score, depending on the metric type requirements.
Pseudo code for building a linear regression model using scikit-learn:
# Import all the necessary libraries #import your dataset dataset= pd.read_csv(“example.csv”) #specify your input and output variables based on your data, varies on different datasets X= dataset.iloc[:,[2,3]].values Y= dataset.iloc[:,4].values #Split the data into training and testing set X_train,X_test,y_train,y_test=train_test_split(X,Y, test_size=0.2,random_state=42) #Perform feature scaling sc_X=StandardScaler() X_train=sc_X.fit_transform(X_train) X_test=sc._X.fit_transform(X_test) #Fit linear regression model to the data from sklearn.linear_model import LogisticRegression classifier=LogisticRegression() classifier.fit(X_train,y_train) #predict results using testing set y_pred=classifier.predict(X_test) #Evaluate your results using metrics, here confusion matrix is being used from sklearn.metrics import confusion_matrix cm=confusion_matrix(y_test,y_pred)
Conclusion:
Congratulations! In this article you have learned the basic concepts behind a logistic regression model. Learn more about building a logistic regression model on breast cancer analysis using Cloudera Data Science Workbench by completing theBreast cancer analysis using a logistic regression model